Florian Henkel, Stefan Balke, Matthias Dorfer, Gerhard Widmer
Abstract
Score following is the process of tracking a musical performance (audio) in a corresponding symbolic representation (score). While methods using computer-readable score representations as input are able to achieve reliable tracking results, there is little research on score following based on raw score images. In this paper, we build on previous work that formulates the score following task as a multi-modal Markov Decision Process (MDP). Given this formal definition, one can address the problem of score following with state-of-the-art deep reinforcement learning (RL) algorithms. In particular, we design end-to-end multi-modal RL agents that simultaneously learn to listen to music recordings, read the scores from images of sheet music,and follow the music along in the sheet. Using algorithms such as synchronous Advantage Actor Critic (A2C) and Proximal Policy Optimization (PPO), we reproduce and further improve existing results. We also present first experiments indicating that this approach can be extended to track real piano recordings of human performances. These audio recordings are made openly available to the research community, along with precise note-level alignment ground truth.
Score Following Markov Decision Process
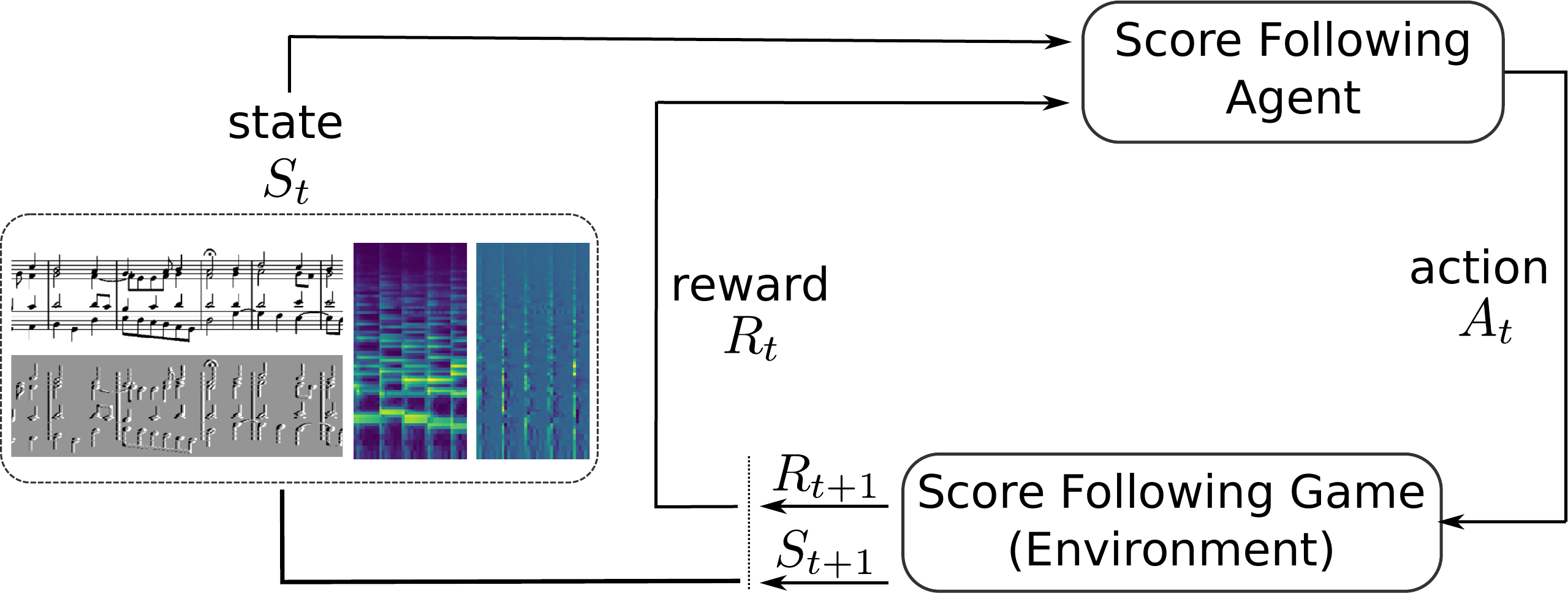
Sketch of the score following MDP. The agent receives the current state of the environment
and a scalar reward signal
for the action taken in the previous time step.
Based on the current state it has to choose an action (e.g., decide whether to increase, keep or decrease its speed in the score) in order to maximize
future reward by correctly following the performance in the score.
Exploring the agent's behavior
While our results show the potential of RL on the score following task, we were curious what our agents actually learned. To this end, we take a closer look on how a trained agent organises the state space internally by looking at a t-SNE projection of the embedding space. Additionally, we want to know what exactly causes the agent to act in a certain way. In order to do this, we apply a technique called integrated gradients, allowing us to find out which parts of the input were influential in the prediction of a certain action.
A Look into the Embedding Space

After visually exploring the data, we emphasize three clusters. The first cluster (C1) in the upper left corner turns out to comprise the beginnings of pieces.
The value of those states is in general high, which is intuitive as the agent can expect the cumulative future reward of the entire pieces.
Note that the majority of the remaining embeddings have a similar value.
The reason is that all our agents use a discounting factor γ < 1 which limits the temporal horizon of the tracking process.
This introduces an asymptotic upper bound on the maximum achievable value.
The second cluster (C2) on the right end corresponds to the piece endings.
Here we observe a low value as the agent has learned that it cannot accumulate more reward in such states due to the fact that the piece ends.
The third cluster (C3) is less distinct. It contains mainly states with a clef somewhere around the middle of the score excerpt.
(These are the result of our way of “flattening” our scores by concatenating single staff systems into one long unrolled score.)
We observe mixed values that lie in the middle of the value spectrum.
A reason for this might be that these situations are hard for the agent to track accurately,
because it has to rapidly adapt its reading speed in order to perform a “jump” over the clef region.
This can be tricky, and it can easily happen that the agent loses its target shortly before or after such a jump.
Thus, the agent assigns a medium value to these states.
A Look into the Policy
In the following, you will see the performance of our best agent on four pieces from the MSMD test split. In the left part of the video, we visualize the integrated gradients on the score and spectrogram excerpt. In case you want to see more videos, please check out our GitHub repo where we provide you with a script to create them yourself. (The last note in the videos is not played as the end of a song is internally defined as the last onset.)
Johann André - Sonatine
While the agent is able to track this piece until the end, we can see that it struggles a little with repetitive musical structures. Starting around 39 seconds, the agent is often ahead when the left hand plays a repeating pattern.L. v. Beethoven - Piano Sonata (Op. 79, 1st Mvt.)
For this fast piece we can see that our agent struggles after encountering a note clef followed by a fast note run.W. A. Mozart - Piano Sonata (KV331, 1st Mvt., Var. 1)
This fast paced piece is not a problem for the agent. If the agent is too far behind or ahead after a note clef, it is able to speed up, slow down or even wait.Pyotr Tchaikovsky - Morning Prayer (Op. 39, No. 1)
The agent is also able to follow along slow pieces quite accurate.Citation
@article{HenkelBDW19_ScoreFollowingRL_TISMIR,
title={Score Following as a Multi-Modal Reinforcement Learning Problem},
author={Henkel, Florian and Balke, Stefan and Dorfer, Matthias and Widmer, Gerhard},
journal={Transactions of the International Society for Music Information Retrieval},
volume={2},
number={1},
year={2019},
doi={http://doi.org/10.5334/tismir.31},
publisher={Ubiquity Press}
}
Acknowledgments
This project received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program(grant agreement number 670035, project CON ESPRESSIONE).

